
데이터가 얼마나, 어떻게 퍼져있는가
Table of Contents
산포도 (Dispersion)
산포도(Dispersion)는 데이터가 평균을 중심으로 얼마나 퍼져 있는지를 나타내는 지표입니다. 같은 평균을 가진 두 데이터 집합이라도 산포도가 다르면 데이터의 분포 특성이 달라질 수 있습니다. 대표적인 산포도의 지표로는 분산(Variance), 표준편차(Standard Deviation), 범위(Range), 사분위수(Quartiles)가 있습니다.
분산 (Variance)
데이터가 평균에서 얼마나 퍼져있는가
분산은 데이터가 평균을 기준으로 얼마나 퍼져 있는지를 나타내는 값으로, 개별 값이 평균에서 얼마나 떨어져 있는지를 제곱하여 평균낸 값입니다. 단위가 원래 데이터의 제곱 형태이기 때문에 해석이 어렵다는 단점이 있습니다.
계산 공식
| 모집단 분산(σ²) = (Σ (X – μ)²) / N |
| 표본 분산(s²) = (Σ (X – X̄)²) / (n – 1) |
예시
| 학생 5명의 점수: 70, 80, 90, 85, 95 평균 = 84 편차 제곱합 = (70-84)² + (80-84)² + (90-84)² + (85-84)² + (95-84)² 표본 분산 = 편차 제곱합 ÷ (5-1) = 78.5 |
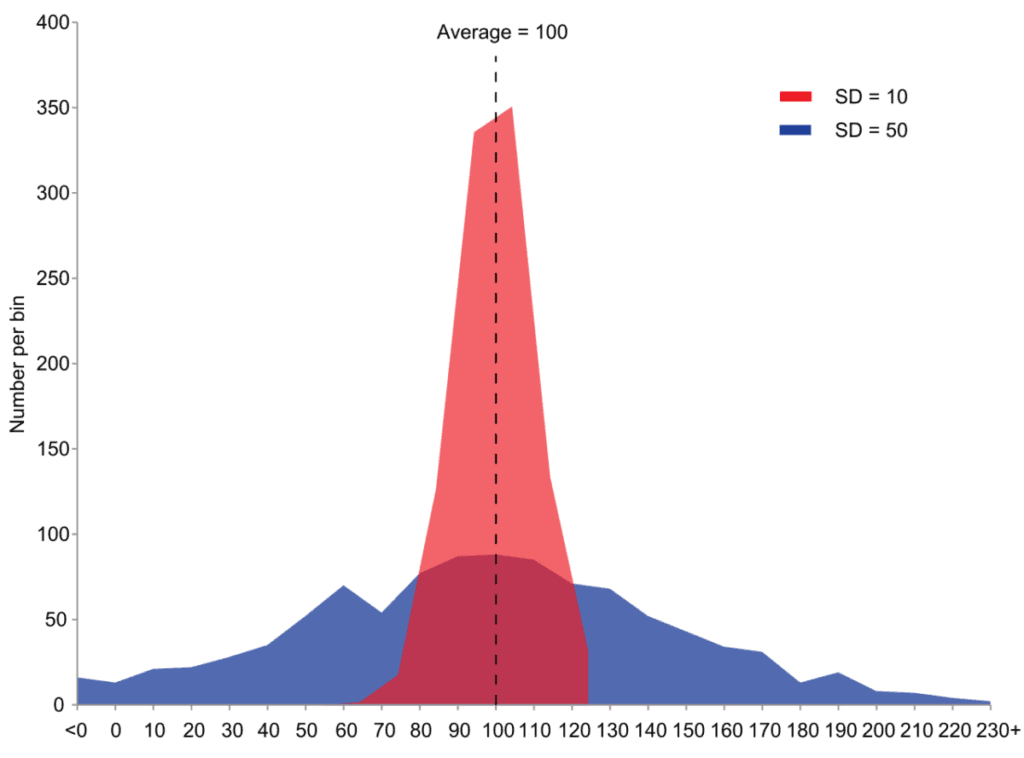
위 그래프는 평균은 같지만 분산은 다른 두 확률 분포를 나타냅니다. 빨간색 분포는 100의 평균값과 100의 분산값을 가지고, 파란색 분포는 100의 확률값과 2500의 분산값을 가집니다. SD는 표준편차를 의미한다.
표준편차 (Standard Deviation, SD)
분산의 제곱근, 데이터의 평균적인 변동 정도
표준편차는 분산의 제곱근을 의미하며, 데이터의 평균과 실제 값 간의 평균적인 차이를 나타냅니다. 데이터의 단위와 동일하기 때문에 해석이 용이하며, 값이 클수록 데이터가 더 넓게 퍼져 있다는 것을 의미합니다.
계산 공식
| 표준편차 (σ or s) = √(분산) |
예시
| 위의 분산 값 78.5의 표준편차 = √78.5 ≈ 8.86 |
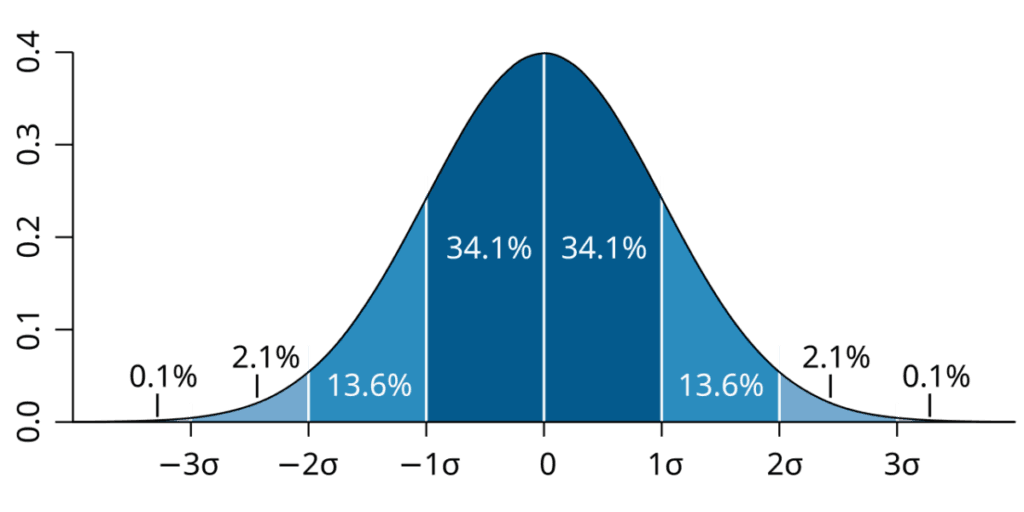
각 밴드의 너비가 1 표준편차인 정규 분포의 그래프입니다.
범위 (Range)
최댓값- 최솟값 , 데이터가 얼마나 넓게 퍼져있는가
범위는 데이터에서 가장 큰 값과 가장 작은 값의 차이를 의미합니다. 쉽게 계산할 수 있지만, 극단값(Outlier)의 영향을 크게 받는다는 단점이 있습니다.
계산 공식
| 범위 = 최대값 – 최소값 |
예시
| 학생 5명의 점수: 70, 80, 90, 85, 95 범위 = 95 – 70 = 25 |
사분위수 (Quartiles)
데이터를 4등분해서 데이터의 분포를 요
사분위수는 데이터를 4등분하여 분포를 분석하는 방법입니다. 특히 중앙값을 포함하여 데이터의 퍼짐 정도를 파악하는 데 유용합니다.
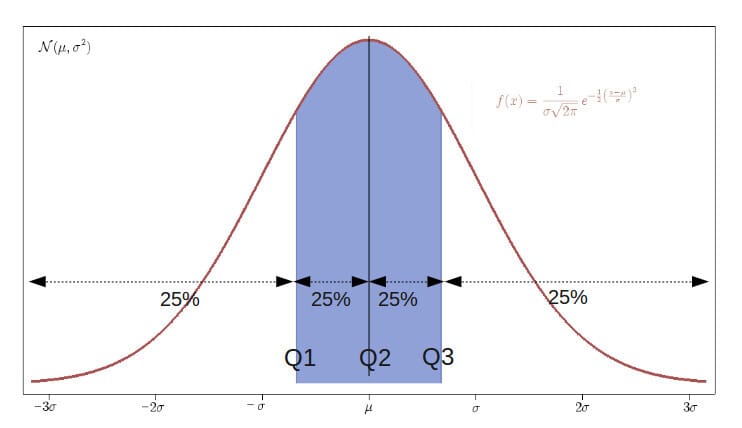
사분위수의 종류
| 제1사분위수(Q1) |
| : 하위 25%에 해당하는 값. |
| 제2사분위수(Q2, 중앙값) |
| : 전체 데이터의 중간 값. |
| 제3사분위수(Q3) |
| : 상위 25%에 해당하는 값. |
| 사분위 범위(IQR, Interquartile Range) |
| : Q3 – Q1로 계산되며, 중앙 50%의 데이터 범위를 의미함. |
예시
| 학생 7명의 점수: 60, 70, 75, 80, 85, 90, 100 |
| Q1 = 70, Q2 = 80, Q3 = 90 |
| 사분위 범위 (IQR) = 90 – 70 = 20 |
산포도의 비교
| 구분 | 분산 | 표준편차 | 범위 | 사분위수 |
| 의미 | 데이터의 평균과의 거리 제곱의 평균 | 분산의 제곱근 | 최대값과 최소값의 차이 | 중앙 50%의 데이터 범위 |
| 극단값 영향 | 영향 있음 | 영향 있음 | 매우 큼 | 영향 적음 |
| 해석 용이성 | 어려움 | 쉬움 | 매우 쉬움 | 중간 |
| 사용 예시 | 정확한 분포 분석 | 데이터 변동성 비교 | 대략적인 데이터 분포 확인 | 이상값 탐지 및 비교 |
정리
산포도는 데이터가 얼마나 퍼져 있는지를 나타내며, 연구의 신뢰성을 평가하는 데 중요한 역할을 합니다. 분산과 표준편차는 데이터의 변동성을 정량적으로 측정하며, 범위는 빠르게 데이터 분포를 확인하는 데 유용하지만 극단값의 영향을 받을 수 있습니다. 사분위수는 극단값의 영향을 줄이고 데이터를 비교하는 데 유용합니다. 연구 목적에 따라 적절한 산포도 지표를 선택하는 것이 중요합니다.
Resource
- Two samples with the same mean and different standard deviations. By JRBrown – 자작, Public Domain, https://commons.wikimedia.org/w/index.php?curid=10777712
- Normal Distriburtion curve that Illustrates Standard Deviations . By M. W. Toews – 자작, based (in concept) on figure by Jeremy Kemp, on 2005-02-09, CC BY 2.5, https://commons.wikimedia.org/w/index.php?curid=1903871
- Normal distribution. Shows the quartile and interquartile range of a normal distribution. By Iqr.png: Ark0nderivative work: Gato ocioso (talk) – Iqr.png, CC BY-SA 3.0, https://commons.wikimedia.org/w/index.php?curid=14702157

