PDF 📄
기술 통계 01. 중심 경향치 (Central Tendency) - 평균, 중앙값, 최빈값

자료 데이터 분포의 중심을 보여주는 값
자료 전체를 대표할 수 있는 값

중심 경향치 (Central Tendency)

중심 경향치(Central Tendency)는 데이터의 대표적인 값을 찾아내는 방법으로, 주어진 자료에서 일반적인 경향을 파악하는 데 사용됩니다. 주로 평균(Mean), 중앙값(Median), 최빈값(Mode)이 중심 경향치를 나타내는 대표적인 지표입니다.

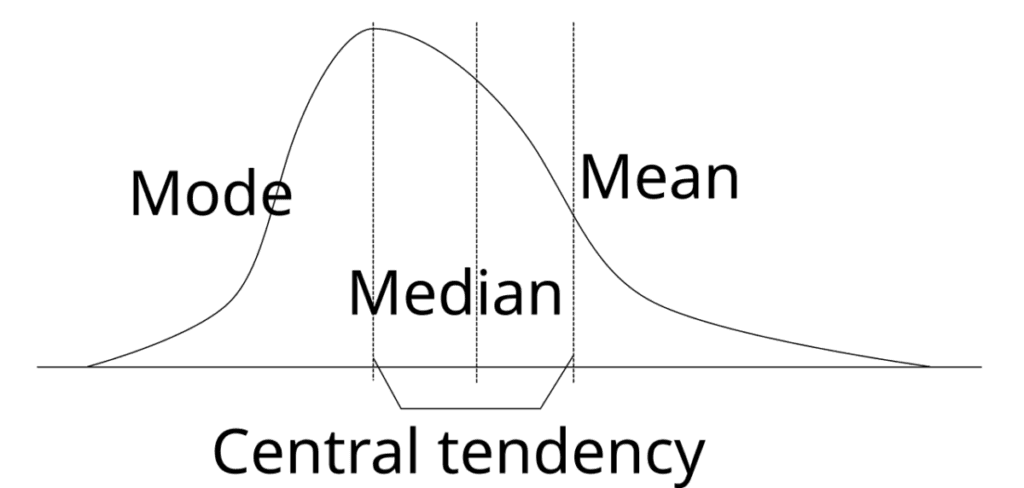
Central Tendency By Pk0001 – 자작, CC BY-SA 4.0, https://commons.wikimedia.org/w/index.php?curid=82179456

평균 (Mean)

모든 값을 더한 후 전체 개수로 나눔.

평균은 데이터의 모든 값을 더한 후, 데이터 개수로 나눈 값입니다. 데이터가 균등하게 분포되어 있을 때 대표값으로 적절하지만, 극단값(아웃라이어, Outlier)에 영향을 많이 받는다는 단점이 있습니다.

모든 데이터 값을 더한 후, 전체 개수로 나눈 값.
산술 평균(Arithmetic Mean):
평균 = (모든 데이터의 합) ÷ (데이터 개수)

예시

학생 5명의 시험 점수: 70, 80, 90, 85, 95
-> 평균 = (70 + 80 + 90 + 85 + 95) ÷ 5 = 84
직원 5명의 월급(단위: 만원): 300, 320, 280, 500, 290
-> 평균 = (300 + 320 + 280 + 500 + 290) ÷ 5 = 338

중앙값 (Median)

크기 순 정렬 시 한 가운데 위치한 값

중앙값은 데이터를 크기 순으로 정렬했을 때, 한가운데 위치한 값입니다. 평균과 달리 극단값)의 영향을 덜 받는다는 장점이 있습니다.

데이터를 크기 순으로 정렬했을 때, 가운데 위치한 값.
– 데이터 개수가 홀수일 때: 한가운데 값이 중앙값.
– 데이터 개수가 짝수일 때: 가운데 두 값의 평균이 중앙값.

예시

학생 5명의 시험 점수: 70, 80, 85, 90, 95
정렬 후: 70, 80, 85, 90, 95
중앙값 = 85
직원 6명의 월급(단위: 만원): 250, 270, 300, 320, 500, 600
정렬 후: 250, 270, 300, 320, 500, 600
중앙값 = (300 + 320) ÷ 2 = 310

최빈값 (Mode)

가장 많이 나타나는 값

최빈값은 데이터에서 가장 많이 나타나는 값을 의미합니다. 평균과 중앙값과 달리, 최빈값은 한 개 이상 존재할 수 있으며, 모든 데이터에서 최빈값이 존재하는 것은 아닙니다.

데이터에서 가장 자주 나타나는 값.
최빈값이 하나만 있는 경우: 단일 최빈값 (Unimodal).
최빈값이 여러 개 있는 경우: 다중 최빈값 (Multimodal).
모든 값이 동일한 빈도로 나타날 경우: 최빈값 없음.

예시

학생 6명의 시험 점수: 70, 80, 80, 90, 95, 100
최빈값 = 80 (가장 많이 등장한 값)
학생 7명의 시험 점수: 60, 70, 70, 80, 90, 90, 100
최빈값 = 70, 90 (두 개의 최빈값이 있음, 다중 최빈값)

중심 경향치 비교

구분평균중앙값최빈값
계산 방식모든 데이터를 더한 후 개수로 나눔순서대로 정렬한 후 가운데 값가장 자주 등장하는 값
극단값에 의한 영향큰 영향 받음거의 영향 없음영향 없음
사용 예시평균 소득, 평균 점수중위 소득, 주택 가격 분석가장 인기 있는 제품, 소비자 선호도

정리

평균, 중앙값, 최빈값은 데이터의 중심을 표현하는 방법이지만, 각각의 특성과 장단점이 다릅니다. 평균은 전체적인 경향을 쉽게 파악할 수 있지만 극단값의 영향을 받을 수 있습니다. 중앙값은 극단값의 영향을 덜 받기 때문에 소득 분포나 주택 가격과 같은 자료 분석에 유용합니다. 최빈값은 가장 자주 등장하는 값을 찾을 때 사용되며, 제품 선호도 조사 등에서 활용됩니다. 연구 목적에 따라 적절한 중심 경향치를 선택하는 것이 중요합니다.

Resource

BIOSTATISTICS, 의통계학